又复习了一下glTF模型，发现了一个很好的英文教程，讲解的非常详细。没有图形学知识背景的人也可以听懂。学习的时候，就顺便翻译成中文，来和大家分享。当然，更推荐看英文教程。

Scenes 和 nodes

Scenes

在一个glTF文件中可能存在多个场景，但在许多情况下，通常只有一个场景，也就是默认场景。每个场景包含 nodes的数组，它们是场景图的根节点的ID。同样的，glTF文件中可以存在多个根节点形成不同的层次，但是在许多情况下，场景将具有单个根节点。最简单也是最可能的场景描述已经在前面的部分中给出，包括具有单个节点的单个场景：

  "scenes" : {
    "scene0" : {
      "nodes" : [ "node0" ]
    }
  },
  "nodes" : {
    "node0" : {
      "meshes" : [ "mesh0" ]
    }
  },

Nodes 构成了场景图

每个 node可以包含一个名为 children的数组，其中包含其子节点的ID。因此，每个节点是节点层次结构中的一个元素，它们一起将场景的结构定义为场景图。

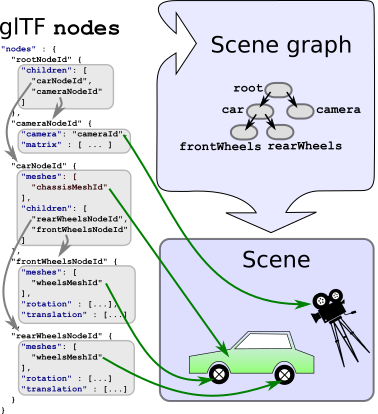java-javascript 图 4a: 场景图

可以遍历 scene 中给出的每个节点，递归地访问其所有子节点，以处理附加到节点的所有元素。该遍历的简化伪代码看起来如下：

traverse(node) {
    // Process the meshes, cameras, etc. that are
    // attached to this node - discussed later
    processElements(node);

    // Recursively process all children
    for each (child in node.children) {
        traverse(child);
    }
}

实际上，遍历需要一些额外的信息：在处理连接到节点的一些元素时，需要知道它们连接到哪个节点。另外，关于节点的变换的信息必须在遍历期间被累积。

局部和全局变换

每个节点可以有一个变换。这种变换将定义平移，旋转或缩放。此变换将应用于连接到节点本身及其子节点的所有元素。因此，节点的层次结构允许构建应用于场景元素的平移，旋转和缩放。

节点的局部变换

对于节点的局部变换可能存在不同的表示。变换可以直接由节点的 Matrix 给出。该矩阵包含16个浮点数，按列优先存放。例如，以下矩阵描述了缩放（2,1,0.5），围绕x轴的旋转约30度以及平移（10,20,30）：

"node0": {
    "matrix": [
        2.0,    0.0,    0.0,    0.0,
        0.0,    0.866,  0.5,    0.0,
        0.0,   -0.25,   0.433,  0.0,
       10.0,   20.0,   30.0,    1.0
    ]
}    

这里定义的矩阵表示如下

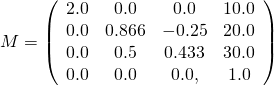java-javascript 图 4b: 一个示例矩阵

节点的变换也可以使用节点的 transform, rotation 和 scale 属性给出 - 有时缩写为TRS：

"node0": {
    "translation": [ 10.0, 20.0, 30.0 ],
    "rotation": [ 0.259, 0.0, 0.0, 0.966 ],
    "scale": [ 2.0, 1.0, 0.5 ]
}

这些属性中的每一个都可以用于创建矩阵，然后这些矩阵的乘积是节点的局部变换：

translation 只包含x，y，z方向的平移。比如，一个 [ 10.0, 20.0, 30.0 ] 平移可以创建出如下矩阵：

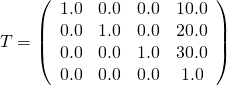java-javascript 图 4c:一个平移矩阵

rotation 以 四元数的形式给出。四元数的数学背景超出了本教程的范围。你只要知道，四元数可以围绕任意轴旋转任意角度。例如，四元数 [0.259,0.0,0.0,0.966] 描述围绕x轴旋转约30度。因此，这个四元数可以转换为旋转矩阵：

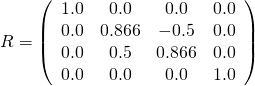java-javascript 图 4d: 一个旋转矩阵

scale 包含沿着x，y和z轴的缩放因子。可以通过把这些缩放因子作为矩阵对角线上的元素来创建相应的矩阵。例如，缩放因子 [2.0,1.0,0.5] 对应的矩阵是：

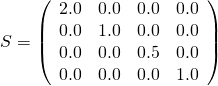java-javascript 图 4e: 一个缩放矩阵

将这些矩阵相乘，以计算节点的最终变换矩阵。相乘的顺序是很重要的。局部变换矩阵总是以 M = T * R * S 的形式计算。这里的 T 表示 translation ； R 表示 rotation ； S 表示 scale。伪代码表示如下：

translationMatrix = createTranslationMatrix(node.translation);
rotationMatrix = createRotationMatrix(node.rotation);
scaleMatrix = createScaleMatrix(node.scale);
localTransform = translationMatrix * rotationMatrix * scaleMatrix;

对于上面给出的示例矩阵，节点的最终局部变换矩阵将是

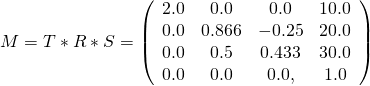java-javascript 图 4f: 由TRS计算而来的最终局部变换矩阵

这个矩阵将导致网格的顶点根据 scale，rotation 和 translation属性被缩放，旋转然后平移。

当节点既不包含Matrix属性也不包含TRS属性时，其局部变换将是单位矩阵。

节点的全局变换

无论JSON文件中的表示形式如何，节点的局部变换都可以存储为4x4矩阵。节点的全局变换由从根节点到相应节点的路径上的所有局部变换的乘积给出：

                     local transform      global transform
root                 R                    R
 +- nodeA            A                    R*A
     +- nodeB        B                    R*A*B
     +- nodeC        C                    R*A*C

注意，全局变换 不能 在文件加载后只计算一次。稍后，你将会看到animations如何修改单个节点的局部变换。这些修改将影响所有后代节点的全局变换。因此，当需要节点的全局变换时，必须从所有节点的当前局部变换直接计算。或者，可以通过缓存全局变换来改进性能，一旦检测到祖先节点的局部变换发生变化，在必要时更新全局变换。具体的实现将取决于编程语言和客户端应用程序的要求，这超出了本教程的范围。

著作权声明

作者陈兴旺，首次发布于 WunWun Blog，转载请保留以上链接

场景和节点

glTF系列教程04