从0和1说起
前段时间在知乎上看到一个有趣的问题：装满的硬盘中是 1 多还是 0 多？整天跟互联网上丰富的信息（视频，音频，图片···）打交道，竟忘了这些丰富的信息都是由 0 和 1 构成的。今天就简单地聊聊计算机中的编码。
说到编码，人们最熟悉还是十进制，因为人有10个手指。想一想，你小时候最开始学加减的时候，是不是掰着手指头算的。但是计算机没有“10个手指头”，计算机浑身上下只有一堆晶体管，晶体管有高电压或低电压，所以在存储和处理信息时，用二进制比较好，这就是 0 和 1 。
但是怎么用二进制表示“二”呢？回答这个问题前，我们先来看一下十进制是如何表示“十”的。十进制中，当数到十时，0,1,2,3,4,5,6,7,8,9···单独的一位数不够用了，人们就把两位组合在一起，并规定第二位上的数代表“十”，这就是“权”的概念。0,1,2,3,4,5,6,7,8,9，10,11,12···97,98,99···单独的两位数不够用了，人们就把三位组合在一起，并规定第三位上的数代表“百”。以此类推，我们也可以把这种方法应用到二进制中去。
二进制 十进制
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 10
无符号数
前面我们已经看到：把位组合在一起，再加上某种解释，即给不同的位“位置”赋予含义，我们就能表示任何有限集合的元素。计算机中就是用这种方法来表示无符号数。无符号数是基于传统的二进制表示法，表示大于或者等于零的数字。
假设一个整数数据类型有w位，每位上的数字为0或1。那么[00···0]就是表示出的最小值（0），[11···1]为表示出的最大值（2^w - 1），介于0~2^w - 1之间的数都有唯一一个w位的编码。
补码
那么如何在计算机中表示负数呢？要知道，计算机中只有0和1，是没有负号“-”的。这就是补码的由来。很多国内的计算机书籍在介绍补码时是这样说的，为了表示有符号数，将最高位解释为符号（0表示正数，1表示负数）。这是不对的,因为这样不能解释-1的补码是[1111]，而不是[1001]。按照这种错误的说法，[1001]中，高位的1表示负号，低位的1表示数值1，于是得出[1001]表示-1.
其实，字的最高位不单单表示符号，它是有权重的！权重为-2^（w-1）。先看几个例子。
[0001] = -0*2^3 + 0*2^2 + 0*2^1 + 1*2^0 = 0+0+0+1 = 1
[0101] = -0*2^3 + 1*2^2 + 0*2^1 + 1*2^0 = 0+4+0+1 = 5
[1011] = -1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 =-8+0+2+1 =-5
[1111] = -1*2^3 + 1*2^2 + 1*2^1 + 1*2^0 = 1+1+1+1 =-1
考虑一下w位补码所能表示的值的范围。[100···0]表示最小值(-2^(w-1))。[011···1]表示最大值(2^(w-1)-1)。
下图是对不同位数的无符号数和有符号数的最大值和最小值的比较。
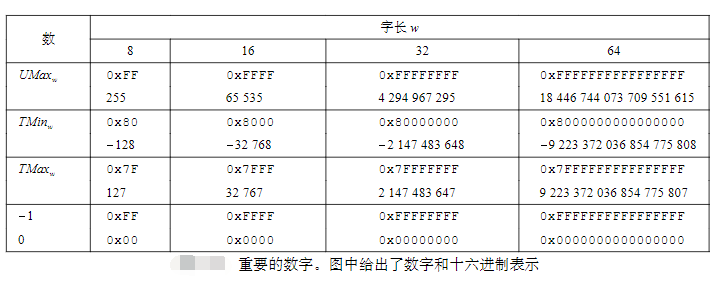无符号数和有符号数的表示范围
无符号加法
在计算机中数的位数确定了，那么相应的最大值也就确定下来了。如果在加法运算过程中，超出最大值怎么办呢？
比如，考虑一个4位数字表示，x = 10和y = 12的位表示分别为[1010]和[1100]。它们的和是22，5位的表示为[10110]。但是我们这里只有4位数，没有办法表示第5位，只能舍弃第5位，将结果表示成[0110]。像这样，完整的整数结果不能放到数据类型的字长限制中去，就叫算术运算溢出。
结论：无符号运算可以被视为一种模运算形式。无符号加法等价于结果和模上2^w。
